Efficient matrix multiplication on a GPU involves two key strategies: (1) computation of output matrix valules in parallel, and (2) managing data movement to minimize slower memory accesses, such as those from global memory, while maximizing the use of faster memory accesses from shared memory (SMEM) and registers. I'll discuss how these strategies are implemented. There are excellent resources about MMUL optimization, such as Simon Boehm's MMUL worklog, Lei Mao's blog post, and the CS508 course, all of which were key references for these notes. I wrote them because understanding efficient MMUL reveals several parallel computing concepts, and writing helps cement my understanding.

Parallelization in MMUL

For MMUL \(C = AB\), we can compute each output value \(C[i,j] = \langle A[i,:], B[:,j] \rangle\) in parallel for all pairs \((i,j)\). The operation's time is spent doing: (1) memory accesses (reading \(A\) and \(B\) elements from global memory and writing \(C\) elements to it), and (2) computation (the multiply-add operations required for \(\langle A[i,:], B[:,j] \rangle\)). For example, an H100 SXM allows global memory accesses at 3 TB/second, and can perform 120 TFLOPS/second (for BF16).

Here is an implementation of parallelized MMUL for square matrices, where each thread computes a single element of matrix \(C\).

	__global__ void simpleMMUL(float* A, float* B, float* C) {
	    int row = threadIdx.y + blockIdx.y*blockDim.y;
	    int col = threadIdx.x + blockIdx.x*blockDim.x;
	    float result = 0.0f;
	    for (int i = 0; i < SIZE; i++) {
		result += A[row*SIZE + i]*B[i*SIZE + col];
	    }
	    C[row*SIZE + col] = result;
	}
		

Memory Hierarchy in GPUs and Data Reuse

GPU memory is organized in a hierarchy: from the largest and slowest (global memory) to the smallest and fastest (registers), with shared memory in the middle. Awareness of this hierarchy helps us reduce time spent in memory accesses - we want to keep data that is accessed frequently, in the fastest possible memory. For example, in computing the \(i^{th}\) row of \(C = AB\), we'll reuse A[i,:] as many times as the number of columns in \(B\). Instead of reading elements of A[i,:] each time from global memory, we could keep them in faster shared memory (which can be accessed by all threads in a thread block). This brings us to our first optimization - shared memory tiling.

Shared Memory Tiling

We want to move data that is accessed frequently, once from global memory (GMEM) to shared memory (SMEM), and then access it from the faster SMEM every time we need it. One consideration is that GMEM is much larger than SMEM, e.g. H100 SXMs offer 80GB GMEM and only 228KB SMEM (per streaming multiprocessor). This limits the amount of data we can move from GMEM to SMEM, and so we move data in chunks (known as "tiles").

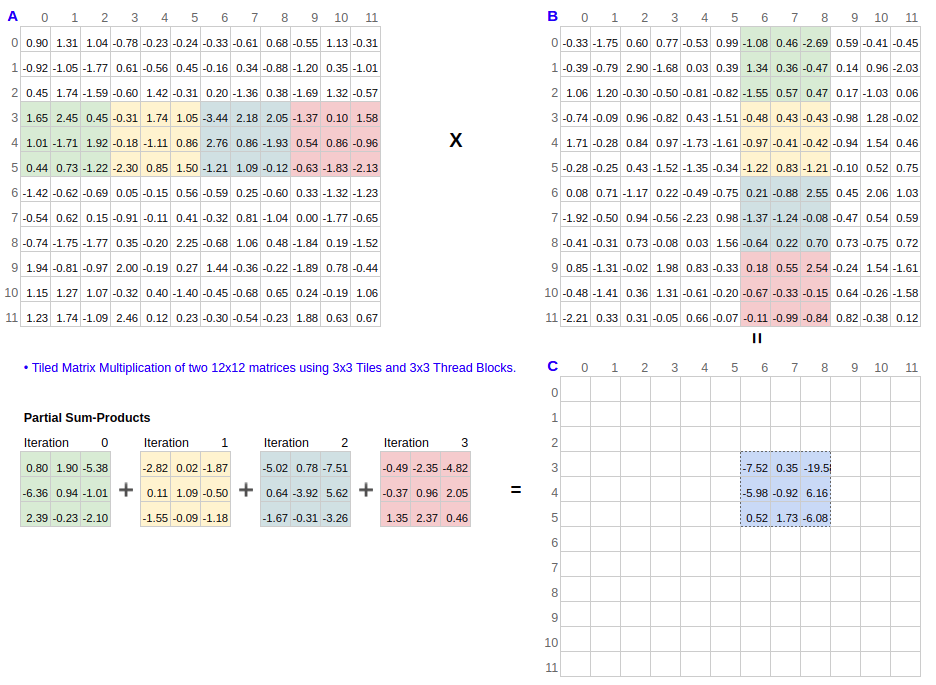
Here is the kernel for tiled MMUL for square matrices with shape (SIZE, SIZE). This setup is best understood with the help of an example. Figure 1 shows MMUL of two 12x12 matrices \(C=AB\) (see my spreadsheet which reproduces Fig. 1). It shows computation performed by a single 3x3 thread block, which is responsible for computing a single 3x3 output tile C[3:6,6:9] (which equals MMUL(A[3:6,:], B[:,6:9]). In Fig. 1, the thread block slides a 3x3 tile over each of A[3:6,:] and B[:,6:9] over four iterations. In each iteration (shown with a distinct color in Fig. 1), the thread block loads a 3x3 tile of each of \(A\) and \(B\) from global memory to SMEM. Since SMEM is shared between all threads in a block, each of the 9 threads in this block can read all elements in the \(A\) and \(B\) tiles. In each iteration, once data loading into SMEM completes, the block multiplies the two tile matrices and accumulates the resulting output. Since we have 9 threads in the block and 9 elements in the output tile, each element is computed in parallel, with all read accesses from SMEM.

	__global__ void smemTiledMMUL(float *A, float *B, float *C) {
	    __shared__ float adata[TILE_SIZE][TILE_SIZE];
	    __shared__ float bdata[TILE_SIZE][TILE_SIZE];

	    int ty = threadIdx.y;
	    int tx = threadIdx.x;
	    int output_row = threadIdx.y + blockIdx.y*blockDim.y;
	    int output_col = threadIdx.x + blockIdx.x*blockDim.x;

	    float result = 0.0f;

	    for (int i = 0; i < SIZE; i += TILE_SIZE) {
		// read data into SMEM
		adata[ty][tx] = A[output_row*SIZE + (i + tx)];
		bdata[ty][tx] =  B[(i + ty)*SIZE + output_col];

		// pause until all threads in block have read into SMEM
		__syncthreads();

		// compute partial result
		for (int j = 0; j < TILE_SIZE; j++) {
		    result += adata[ty][j]*bdata[j][tx];
		}

		// pause until all threads in block are done reading from SMEM
		__syncthreads();
	    }
	    C[output_row*SIZE + output_col] = result;
	}
		

Data Reuse and Rectangular Tiles

In our example above, each element of \(A\) and \(B\) is read TILE_SIZE times from SMEM. The tiles need not be square, e.g. if we had strips for tiles, i.e. (TILE_SIZE, 1) shaped tile of \(A\) and (1, TILE_SIZE) shaped tile of \(B\), we would still reuse each element TILE_SIZE times from SMEM (see the strip_input_tiles tab in my spreadsheet for MMUL calculations). That said, degree of data reuse is only one of the few considerations we should look at.

Here is a kernel for tiled MMUL using strip tiles. We observe two points:

• Barriers: In each iteration of the outer for-loop, we compute a single sum-product (compared with TILE_SIZE sum-products in the case of square tiles). We are doing fewer computations for the two __syncthreads() calls that are made in every iteration.
• Idle Threads: We have TILE_SIZE**2 threads in a thread block, but only 2*TILE_SIZE-1 of them are doing the work of loading from global memory to SMEM, while other threads in the block are idle.

	__global__ void smemStripTiledMMUL(float *A, float *B, float *C) {
	    __shared__ float adata[TILE_SIZE];
	    __shared__ float bdata[TILE_SIZE];

	    int ty = threadIdx.y;
	    int tx = threadIdx.x;
	    int output_row = threadIdx.y + blockIdx.y*blockDim.y;
	    int output_col = threadIdx.x + blockIdx.x*blockDim.x;

	    float result = 0.0f;

	    for (int i = 0; i < SIZE; i++) {
		// read data into SMEM
		if (tx == 0) {
		    adata[ty] = A[output_row*SIZE + i];
		}
		if (ty == 0) {
		    bdata[tx] =  B[i*SIZE + output_col];
		}

		// pause until all threads in block have read into SMEM
		__syncthreads();

		// compute partial result
		result += adata[ty]*bdata[tx];

		// pause until all threads in block are done reading from SMEM
		__syncthreads();
	    }
	    C[output_row*SIZE + output_col] = result;
	}
		

We loaded single strips of inputs \(A\) and \(B\) into SMEM in Kernel 3 and TILE_SIZE strips of each on Kernel 2, achieving the same degree of data reuse in each case. We can tune the number of strips loaded to take into account other considerations (such as the two discussed above). See the tab rectangular_input_tiles on my spreadsheet for an example. Note that in all these cases we used square thread blocks and output tiles, each of shape (TILE_SIZE, TILE_SIZE). See the tab rectangular_input_and_output_tiles on the spreadsheet for an example with rectangular input/output tiles (adata of shape \(2 \times 2\), bdata \(2 \times 4\) and output tile \(2 \times 4\)).

I found these slides from UIUC's ECE508 to be very useful, and used them heavily as references for sections on tiling in these notes. I highly recommend looking through ECE508.

Joint SMEM and Register Tiling

A question that comes to mind - just as we moved frequently accessed data from global memory to SMEM, could we move that data further down to the registers? One consideration is that unlike the SMEM which is shared across all threads in a block (all of which can access data residing on their SMEM), registers are exclusive to a thread. In our SMEM Tiling kernels above, every element of adata was read by TILE_SIZE threads to compute partial outputs for TILE_SIZE output locations. If an element of \(A\) is stored in a thread's registers, no other threads will be able to access it. This hints at a possible direction - we could have that thread itself reuse this element of \(A\) multiple times for partial computations of as many number of output locations. This technique is called Thread Coarsening - we tradeoff parallelism (because a single thread will compute multiple output locations sequentially) for faster memory access (from registers).

Note: In all kernels above, we used 2D thread blocks (it was easy to align their indices with our 2D input/output tile indices). In the case of register tiling, we use Thread Coarsening to compute multiple output locations in a single thread, and such alignment is tricky. In all implementations I found on the internet, folks used 1D thread blocks as I believe 1D indices are easier to work with in this case. I'll also use 1D thread blocks in my joint SMEM and register tiling kernel.

Register Pressure and Input/Output Tile Shapes

We have to choose the number of rows in the output tile TSZ_ROWS, number of columns in the output tile TSZ_COLS, and the number of strips loaded in each input tile TSZ_STRIPS. Here are some considerations:

• We choose to coarsen threads along the column dimension of the output tile. In this setup, a single thread will compute an entire row of the output tile. Since we have TSZ_ROWS output tile rows, we can have TSZ_ROWS threads in a thread block (1 for each output tile row).
• Computing a row of the output tile will require repeated (TSZ_COLS to be specific) accesses to each element of the corresponding row of \(A\). The single thread responsible for computing this output tile row can thus load elements of \(A\) in its registers for this repeated access.
• Each thread will have to keep TSZ_COLS partial outputs into its registers. Since registers are a scarce resource (e.g. an H100 SXM GPU has 33MB of total register file size), this limits how large TSZ_COLS can be. This is referred to as "register pressure" in ECE508.
• Entries in a column of the output tile will be computed by different threads, which will be using the same elements of \(B\) for this computation. To facilitate repeated accesses of \(B\) elements by different threads in a block, we will keep them in SMEM.
• How many strips of data should we load in one iteration? If we set TSZ_STRIPS = 1, which means the \(B\) tile in SMEM will be of shape (1, TSZ_COLS), then our TSZ_ROWS threads will be loading TSZ_COLS elements of \(B\) into SMEM. Due to register pressure, TSZ_COLS is lower than TSZ_ROWS, e.g. ECE508 slides recommend 64 rows and 16 columns. This would lead to just one-fourth of our threads (in a block) reading \(B\) from global memory to SMEM. To have all our threads read data into SMEM, we can set TSZ_STRIPS equal to the ratio TSZ_ROWS / TSZ_COLS.

Kernel 4 below implements MMUL with joint SMEM and register tiling.

	__global__ void smemRegisterTiledMMUL(float *A, float *B, float *C) {

	    __shared__ float bdata_smem[TSZ_STRIPS][TSZ_COLS];
	    float adata_regs[TSZ_COLS];
	    float result_regs[TSZ_COLS] = {0.0f};

	    const int tx = threadIdx.x;

	    // map thread index to bdata coordinates (row-major)
	    const int btile_col = tx % TSZ_COLS;
	    const int btile_row = tx / TSZ_COLS;

	    // map thread index to C's row and columns (as 1 thread
	    // will produce TSZ_COLS entries)
	    const int thread_blocks_per_row = SIZE / TSZ_COLS;
	    const int output_row = blockIdx.x / thread_blocks_per_row * blockDim.x + threadIdx.x;
	    const int output_col = blockIdx.x % thread_blocks_per_row * TSZ_COLS;

	    for (int k = 0; k < SIZE; k += TSZ_STRIPS) {
		// read B data into SMEM
		bdata_smem[btile_row][btile_col] = B[(k + btile_row)*SIZE + (output_col + btile_col)];

		// wait for all threads to finish reading into SMEM
		__syncthreads();

		// read A data into registers
		for (int i = 0; i < TSZ_STRIPS; i++) {
		    adata_regs[i] = A[output_row*SIZE + (k + i)];
		}

		// compute partial result
		for (int i = 0; i < TSZ_COLS; i++) {
		    for (int j = 0; j < TSZ_STRIPS; j++) {
			result_regs[i] += adata_regs[j] *  bdata_smem[j][i];
		    }
		}

		// wait for all threads to finish reading from SMEM
		__syncthreads();
	    }

	    for (int i = 0; i < TSZ_COLS; i++) {
		C[output_row*SIZE + (output_col + i)] = result_regs[i];
	    }
	}