Positional information is important for conveying the meaning of a set of words. Consider the phrases good, not bad! and bad, not good! - although they contain the same words, their meanings are opposite due to their positional arrangement.
Sinusoidal Positional Embeddings
In Attention Is All You Need, Vaswani et. al. propose using a predetermined positional embedding for each index in an input sequence. We add the positional embedding \(p_{\text{pos}} \in \mathbb{R}^d\) (here \(d\) is the dimension of hidden states), corresponding to an index \(pos\) to the input embedding \(x_{pos}\) at index \(pos\). Here \(p_{\text{pos}, i}\) is the value of the \(i^{th}\) dimension of the embedding. Specifically, for each of \(t \in \text{{k, q, v}}\) for key, query, and value respectively, we compute a representation \[t_{pos} = f_t(x_{pos}) = W_t(x_{pos} + p_{pos})\] and then use these key, query, value representations to compute attention weights (here \(m,n\) are two position indices in the input sequence of length \(N\)): \[\alpha_{m,n} = \frac{\exp{\left(q_m^Tk_n/\sqrt{d}\right)}}{\sum_{j=0}^{N-1}\exp{\left(q_j^Tk_n/\sqrt{d}\right)}}\]
The sinusoidal positional embedding is defined as: \[p_{\text{pos}, i} = \begin{cases}\sin{\left(pos/10000^{\frac{i}{d}}\right)} & i \text{ is even} \\ \cos{\left(pos/10000^{\frac{i-1}{d}}\right)} & i \text{ is odd}\end{cases}\]
The authors note:
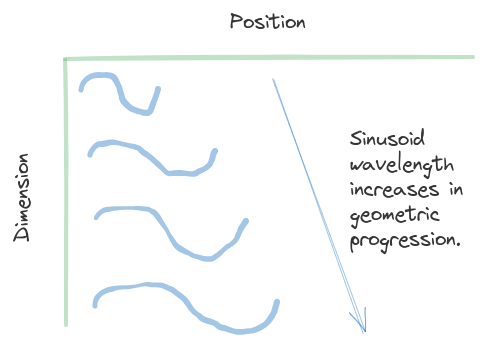
... each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2π to 10000 · 2π
Proof Sketch: For even \(i\), consider \(p_{\text{pos}, i}\). Let the wavelength be \(\lambda\) (i.e., all else being the same, if we change \(pos\) by \(\lambda\), we'll end up with the same value of \(p_{\text{pos}, i}\)). We have: \[ \begin{align} \sin{\left((pos+\lambda)/10000^{\frac{i}{d}}\right)} &= \sin{\left(pos/10000^{\frac{i}{d}} + 2\pi\right)} \\ \implies \lambda &= 2\pi 10000^{\frac{i}{d}} \end{align} \]
As \(i \in \{0, 2, \cdots, d-2\}\) (assuming \(d\) is even), the wavelengths of sinusoids at even indices of the positional embedding will be \(2\pi, 2\pi 10000^{\frac{2}{d}}, \cdots, 2\pi 10000^{\frac{d-2}{d}}\). In a similar manner, we can show that the wavelengths of sinusoids corresponding to odd indices will be this same set \(2\pi, \cdots, 2\pi 10000^{\frac{d-2}{d}}\).
Uniqueness of Sinusoidal Positional embeddings: For a position \(pos\) and some \(k \in \mathbb{Z}^+\) consider the even indices of the positional embeddings \(i=0,2,4,\cdots,d-2\). If \(p_{\text{pos}+k} = p_{\text{pos}}\), then for all even indices \(i\), we have: \[ \sin{\left(\frac{\text{pos}+k}{10000^{i/d}}\right)} = \sin{\left(\frac{\text{pos}}{10000^{i/d}}\right)} \] This implies that for all \(i=0,2,4,\cdots,d-2\), the number \(k/10000^{i/d}\) should be some integer multiple of \(2\pi\). Now for \(i=0\), the expression \(k/10000^{i/d} = k\) which implies that \(k = m\pi\) for some \(m \in \mathbb{Z}\), which means \(k\) is irrational. This contradicts our assumption that \(k \in \mathbb{Z}^+\). Thus we've shown that sinusoidal positional embeddings are indeed unique. Credit to Anthropic's Claude Opus for helping come up with this argument.
The authors Vaswani et. al. note further:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, \(p_{pos+k}\) can be represented as a linear function of \(p_{pos}\).
Proof Sketch: Consider even \(i\), and define \(c_i = 1/10000^{\frac{i}{d}}\) for brevity. We have: \[ \begin{align} p_{pos+k, i} &= \sin{\left(c_i(pos + k)\right)} \\ &= \sin{(c_i pos)}\underbrace{\cos{(c_i k)}}_{a_{k,i}} + \cos{(c_i pos)}\underbrace{\sin{(c_i k)}}_{b_{k,i}} \\ &= a_{k,i}p_{pos, i} + b_{k,i}p_{pos, i+1} \end{align} \] For odd \(i\), we can simiarly show: \[ p_{pos+k, i} = a_{k,i}p_{pos, i+1} - b_{k,i}p_{pos, i} \] Working along these lines, we can represent \(p_{pos+k} = M_kp_{pos}\) where \(M_k \in \mathbb{R}^{d \times d}\) is as follows: \[ M_k = \begin{bmatrix} a_{k,0} & b_{k,0} & 0 & 0 & \cdots & 0 \\ 0 & - b_{k,1} & a_{k,1} & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \end{bmatrix} \] We've shown that \(p_{pos+k}\) can be expressed as a linear transformation of \(p_{pos}\).
I think the reason authors hypothesize that the model can learn to attend to relative positions, is because \(M_k\) does not depend on \(pos\) and just depends on \(k\).
Rotary Positional Embeddings
In RoFormer: Enhanced Transformer with Rotary Position Embedding, Su et. al. propose a position embedding mechanism which incorporates positional information only in the relative form. Sun et. al. (2022) note one reason we want this dependency to be relative and not absolute - we want the represenation of a sequence to be robust to position translation (e.g. arising from left or right padding).
The RoFormer paper discusses (refer Section 2.3) the expansion of the logit term \(q_m^Tk_n\) or \(\langle f_q(x_m), f_k(x_n)\rangle\) used to compute attention weights, and four different experiments documented in literature to modify this term. The authors note that the variant which has proven to be the best depends only on the input embeddings of two positions, and the relative position. Motivated by this, the authors set out to find a replacement for the logit term which explicitly takes the input embeddings \(x_m, x_n\) for two positions, and only the relative position \(m-n\) as input. They set out to solve for \(f_q, f_k\) such that the inner product in the logit term, \(\langle f_q(x_m), f_k(x_n)\rangle\), is of the form \(g(x_m, x_n, m-n)\).
RoPE in 2D
We first consider a toy scenario where our input token embeddings \(x_m, x_n \in \mathbb{R}^2\), i.e. they are vectors in the 2D plane. The authors represent these 2D vectors as complex numbers and perform arithmetic operations, but I think drawing that equivalency is not required for understanding RoPE (complex number arithmetic does help in proving various properties of RoPE, such as showing that value of the inner product decays as relative distance \(|m-n|\) increases; see Section 3.4.3 of the paper). For \(t \in \{q,k\}\):- First, project \(x_m\) to \(y_{t,m} = W_tx_m\). The projection \(y_{t,m} \in \mathbb{R}^2\); say it is the vector \([y^1_{t,m} y^2_{t,m}]^T\).
- Rotate \(y_{t,m}\) counter-clockwise by \(m\theta\) to compute \(t_m = R^m(\theta)y_{t,m}\) where \(R^m(\theta)\) is the rotation matrix: \[R^m(\theta) = \begin{bmatrix} \cos{m\theta} & -\sin{m\theta} \\ \sin{m\theta} & \cos{m\theta} \end{bmatrix}\]
We thus compute query and key vectors by rotating projected input embeddings, i.e. \(q_m = R^m(\theta)\left(W_qx_m\right)\) and \(k_n = R^n(\theta)\left(W_kx_n\right)\). Next we compute the inner product \(\langle q_m, k_n\rangle\). \[ \begin{align} \langle q_m, k_n\rangle &= \left(R^m(\theta)\left(W_qx_m\right)\right)^TR^n(\theta)\left(W_kx_n\right) \\ &= x_m^TW_q^T\underbrace{R^m(\theta)^TR^n(\theta)}_{R^{n-m}(\theta)}W_kx_n \\ &= x_m^TW_q^TR^{n-m}(\theta)W_kx_n \end{align} \] Using authors' proposed form for \(q,k\) we observe that the inner product \(\langle q_m, k_n\rangle\) depends only on relative position \(m-n\) and not on absolute positions.
Choice of \(\theta\): For the \(d=2\) case, authors use \(\theta = \frac{1}{10000}\) (I'll discuss the general case for \(d>2\) dimensions below). We can interpret the inner product term \(\langle q_m, k_n\rangle\) as the inner product between (1) projected input embedding \(W_qx_m\) and (2) projected input embedding \(W_kx_n\) rotated by \(\phi = (n-m)\theta\). For two 2D vectors \(u, v \in \mathbb{R}^2\) with angle \(\phi\) between them, the inner product \(\langle u, v\rangle = |u||v|\cos{\phi}\). The inner product will oscillate as \(\phi\) changes, and will be periodic with period \(2\pi\). This implies that RoPE's choice of inner product will also oscillate as the relative position \(n-m\) increases. This will make it difficult to use RoPE for very long sequence lengths as we'll not observe a monotonically decreasing inner product as relative position increases. Figure 1 in Sun et. al. (2022) confirms this oscillation, and its authors propose a fix for this which I'll discuss below.
RoPE in \(d\) Dimensions
To generalize to \(d\) dimensions, we project input token embedding to \(d\) dimensions again by computing \(y_{t,m} = W_tx_m\) for \(t \in \{q, k\}\). We then apply a 2D rotation matrix \(R^m(\theta_{2i})\) to each consecutive pair \((y_{t,m}^{2i}, y_{t,m}^{2i+1})\) for \(i=0,2,\cdots, d//2-1\) (authors' choose \(\theta_{i} = 10000^{\frac{-2i}{d}}\)). \[ t_m = R_mW_tx_m \\ R_m = \begin{bmatrix} \cos{m\theta_0} & -\sin{m\theta_0} & 0 & 0 & \cdots & 0 & 0 \\ \sin{m\theta_0} & \cos{m\theta_0} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos{m\theta_2} & -\sin{m\theta_2} & \cdots & 0 & 0 \\ 0 & 0 & \sin{m\theta_2} & \cos{m\theta_2} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \cos{m\theta_d} & -\sin{m\theta_d} \\ 0 & 0 & 0 & 0 & 0 & \sin{m\theta_d} & \cos{m\theta_d} \end{bmatrix} \] Higher the dimension index, smaller the rotation angle.
RoPE: Complex Arithmetic
My discussion so far has been in terms of rotation matrics, and for completeness, I'll now show equivalent complex arithmetic for the 2D case. Consider column vectors \(q_m, k_n \in \mathbb{R}^2\) where \(q_m = W_qx_m\) and \(k_n = W_kx_n\). We can map these 2D vectors \([q^1_m, q^2_m], [k^1_n, k^2_n]\) to complex numbers \(q^1_m + jq^2_m\) and \(k^1_n + jk^2_n\). Let's compute the attention inner product using rotation matrices. First we will rotate \(q_m\) by \(m\theta\) and \(k_n\) by \(n\theta\). Next we will compute this inner product between the rotated vectors: \[ \begin{bmatrix} q^1_m\cos{(m\theta)} - q^2_m\sin{(m\theta)} \\ q^1_m\sin{(m\theta)} + q^2_m\cos{(m\theta)} \end{bmatrix}^T \begin{bmatrix} k^1_n\cos{(n\theta)} - k^2_n\sin{(n\theta)} \\ k^1_n\sin{(n\theta)} + k^2_n\cos{(n\theta)} \end{bmatrix} \] Using basic trignometric expansions (e.g. for \(\sin{(a + b)}\)), we can show that this is equivalent to: \[ q^1_mk^1_n\cos{(m-n)\theta} + q^1_mk^2_n\sin{(m-n)\theta} - q^2_mk^1_n\sin{(m-n)\theta} + q^2_mk^2_n\cos{(m-n)\theta} \]
We'll show that this attention equals \(\text{Re}\left[(q^1_m + jq^2_m)(k^1_n + jk^2_n)^*e^{(m-n)\theta}\right]\) where \(^*\) denotes the complex conjugate and \(\text{Re}[\cdot]\) denotes the real part of a complex number. We can show this by writing \(e^{(m-n)\theta} = \cos{(m-n)\theta} + j\sin{(m-n)\theta}\), multiplying the three complex numbers inside \(\text{Re}[\cdot]\) and keeping their real part.