Authors Zhao, Israel et. al. (2024) address the issue of compute wasted in prefilling a transformer with sequence batches with a large number of padding tokens (e.g. when we batch several short sequences with one very long sequence, all the short sequences are padded to match the length of the longest sequence). Long contexts take longer to prefill (see section on Prefilling Latency in my notes).

Prepacking Algorithm

Say we have \(k\) prompts \(p_1,\cdots,p_k\) of lengths \(l_1,\cdots,l_k\) respectively. Here is a high level overview of the authors' approach:

1. Typically we would create a batch of size \(k\) out of these prompt, with each prompt padded to a sequence length \(m = \max_{i=1}^k l_i\). During the forward pass, we'll end up wasting compute on pad tokens (\(m-l_i\) tokens for the \(i^{th}\) sequence).
2. Authors' idea is to fit a short prompt \(m\) (from our set of prompts) into the padding space of another prompt \(n\). This is possible when \(l_m \leq (m-l_n)\). This problem is equivalent to the Bin Packing Problem which is solved using approximation algorithms. Authors use an off-the-shelf solution for this packing. Their formulation: pack the prompts into the smallest possible number of bins, where each bin has size \(m = \max_{i=1}^k l_i\).
3. We want to do a forward pass through such a packed multi-prompt sequence, to get KV caches for each of the \(k\) prompts. Since we've used up space previously occupied by pad tokens, we'll not waste as much compute. There are two issues:
   • A vanilla causal mask typically used in self-attention modules, would not prevent tokens of one prompt \(p_j\) from attending to tokens of a prompt \(p_i\) occuring earlier in the sequence than \(p_j\). Authors fix this by creating masks which ensure that a token attends just to tokens of the same prompt, which occuring at earlier positions.
   • Some positional encodings take into account the absolute position of a token. Authors ensure that positional encodings restart their index for every prompt in a sequence.

Here is the algorithm as it appears in the paper:

Impact

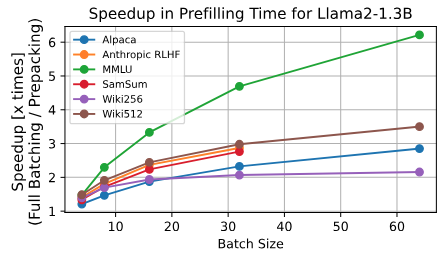
By utilizing memory typically taken up by pad tokens, authors' prepacking approach significantly reduces prefilling memory requirements. This allows up to 16x larger batch sizes while prefilling (tested using the Llama2 1.3B model on the MMLU dataset). Reduced memory requirements allow deployments in low resource environments. Further, prepacking substantially speeds up prefilling. Larger batches exhibit higher speed-ups, probably because they are more likely to have an uneven distribution of prompt lengths. See Figure 6 from the paper below for speed-ups: